Sebagai contoh, kita ambil matriks A2x2
-
- A =
 tentukan determinan A
tentukan determinan A
- A =
-
- detA = ad - bc
Determinan dengan Minor dan kofaktor
-
- A =
 tentukan determinan A
tentukan determinan A
- A =
- detA = ad - bc
- M11 =
 = detM = a22a33 x a23a32
= detM = a22a33 x a23a32
- M11 =
-
- c11 = (-1)1+1M11 = (-1)1+1a22a33 x a23a32
-
- M32 =
 = detM = a11a23 x a13a21
= detM = a11a23 x a13a21
- M32 =
-
- c32 = (-1)3+2M32 = (-1)3+2 x a11a23 x a13a21
-
- det(A) = a11C11+a12C12+a13C13
[sunting] Determinan dengan Ekspansi Kofaktor Pada Baris Pertama
Misalkan ada sebuah matriks A3x3-
- A =

- A =
-
- det(A) = a11
 - a12
- a12 + a13
+ a13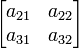
-
- = a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31)
- = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32
-
- det(A) = a11
-
- A =
 tentukan determinan A dengan metode ekspansi kofaktor baris pertama
tentukan determinan A dengan metode ekspansi kofaktor baris pertama
- A =
-
- det(A) =
 = 1
= 1 - 2
- 2 + 3
+ 3 = 1(-3) - 2(-8) + 3(-7) = -8
= 1(-3) - 2(-8) + 3(-7) = -8
- det(A) =
[sunting] Determinan dengan Ekspansi Kofaktor Pada Kolom Pertama
Pada dasarnya ekspansi kolom hampir sama dengan ekspansi baris seperti di atas. Tetapi ada satu hal yang membedakan keduanya yaitu faktor pengali. Pada ekspansi baris, kita mengalikan minor dengan komponen baris pertama. Sedangkan dengan ekspansi pada kolom pertama, kita mengalikan minor dengan kompone kolom pertama.Misalkan ada sebuah matriks A3x3
-
- A =

- A =
-
- det(A) = a11
 - a21
- a21 + a31
+ a31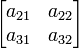
-
- = a11(a22a33 - a23a32) - a21(a21a33 - a23a31) + a31(a21a32 - a22a31)
- = a11a22a33 + a21a23a31 + a31a21a32 - a22(a31)2 - (a21)2a33 - a11a23a32
-
- det(A) = a11
-
- A =
 tentukan determinan A dengan metode ekspansi kofaktor kolom pertama
tentukan determinan A dengan metode ekspansi kofaktor kolom pertama
- A =
-
- det(A) =
 = 1
= 1 - 4
- 4 + 3
+ 3 = 1(-3) - 4(-8) + 3(-7) = 8
= 1(-3) - 4(-8) + 3(-7) = 8
- det(A) =
[sunting] Adjoin Matriks 3 x 3
Bila ada sebuah matriks A3x3-
- A =

- A =
-
- C11 = -12 C12 = 6 C13 = -16
- C21 = 4 C22 = 2 C23 = 16
- C31 = 12 C32 = -10 C33 = 16
-
- adj(A) =

- adj(A) =
[sunting] Determinan Matriks Segitiga Atas
Jika A adalah matriks segitiga nxn (segitiga atas, segitiga bawah atau segitiga diagonal) maka det(A) adalah hasil kali diagonal matriks tersebut-
 = (2)(-3)(6)(9)(4) = -1296
= (2)(-3)(6)(9)(4) = -1296


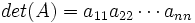
thanks
BalasHapus